Lernauftrag 16: Ursachen für Leistungsänderung

Hier findest die Aufgaben ohne Lösungen.

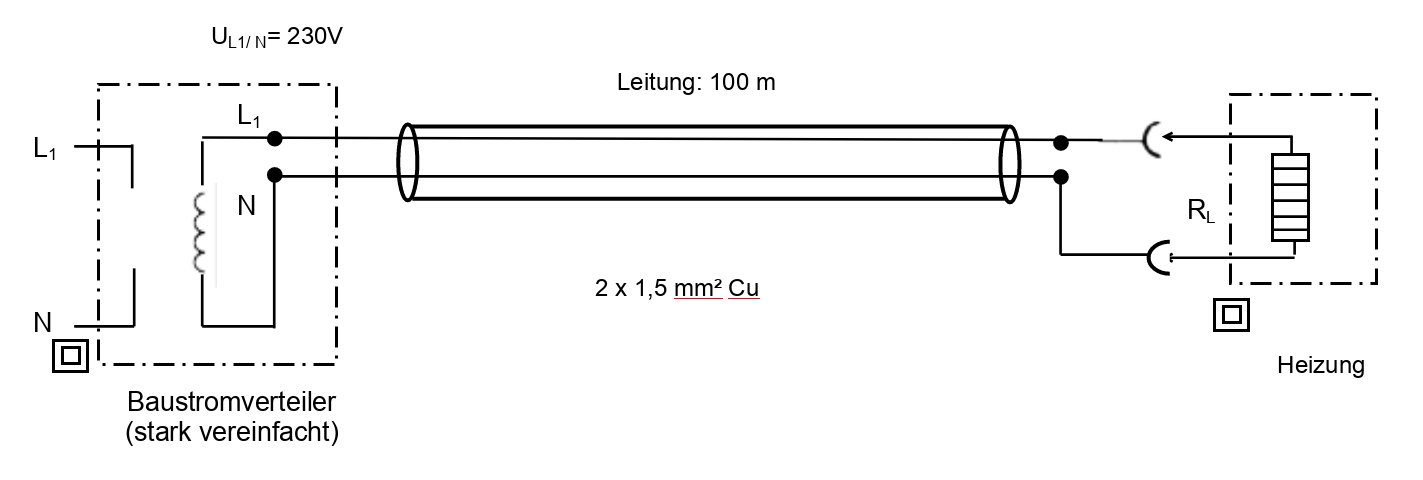
Auf einer Baustelle wurde eine Heizung mit \(230\ V/ 2,6\ kW\) aus einem Baustromverteiler mit elektrischer Energie versorgt. Die Heizung wurde ca. 10 m entfernt von der Verteilung aufgestellt und dort arbeitete sie wie gewünscht.

Nach einer Woche wurde die Heizung abgebaut und auf einer anderen Baustelle erneut aufgebaut. Dieses Mal wurde sie jedoch über eine 100 m lange Anschlussleitung betrieben. Ein Kollege stellte fest, dass die Heizung nicht mehr die volle Leistung abgibt.

Die Heizung wird für diese Aufgabe stark vereinfacht an Gleichstrom betrieben. Die Verlängerungskabel bestehen aus \(2\times 1,5mm^2\ Cu\).

Aufgabe 1

Zeichne* ein Ersatzschaltbild (ESB) der betriebenen Heizungsanlage. Im Kern entspricht die Heizung einem Widerstand.

Ein mögliches Ersatzschaltbild

Aufgabe 2

Berechne die Leistung der Heizung auf beiden Baustellen. Geh davon aus, dass die Heizung

Hilfestellung:
Betrachte zuerst, daß es keine Zuleitung gäbe und die Heizung unmittelbar an der Stromversorgung ist.

Ermittle den fließenden Strom.
Ermittle den Widerstand, den die Heizung immer darstellt.

Nun kommt die Leitung hinzu

Ermittle den Leitungswiderstand bei 10m Entfernung zur Verteilung
Ermittle den Leitungswiderstand bei 100m Entfernung zur Verteilung
Nutze das Tabellenbuch, um die Formel für den Leitungswiderstand zu finden.
Bedenke das Material, aus dem der Leiter ist.

Zuleitung und Heizung sind Widerstände in Reihe.

Addiere sie
Berechne, welcher Strom fließt
Nutze den gefundenen Strom, um die Leistung zu berechnen
Vergleiche die beiden Leistungen

geg:
Leistung \(P=2600\ W\)
Spannung \(U=230\ V\)
Leitung 1 von 10m Länge \(\Rightarrow l_1 = 2\cdot 10\ m=20\ m\)
Leitung 2 von 100m Länge \(\Rightarrow l_2=2\cdot100\ m= 200\ m\)

ges: \(I\), \(R_{Heizung}\), \(R_{Leitung1}\), \(R_{Leitung2}\), \(P_{Leitung1}\), \(P_{Leitung2}\)

Lös:
Strom, welcher durch die Heizung fließt
\(P=U\cdot I\Leftrightarrow I=\frac P U=\frac{2600\ W}{230\ V}=11,3\ A\)

Widerstand der Heizung \(R_{Heizung}\)
\(U=R_{Heizung}\cdot I\Leftrightarrow R_{Heizung}=\frac U I=\frac{230\ V}{11,3\ A}=20,35\ \Omega\)

Widerstand der 10m Leitung \(R_{Leitung1}\)
\(R_{Leitung1}=\rho \cdot \frac l A= 17,86\cdot10^{-3}\ \frac{\Omega\cdot mm^2}{m}\cdot\frac{20\ m}{1,5\ mm^2}=0,238\ \Omega=238\ m\Omega\)

Widerstand der 100m Leitung \(R_{Leitung2}\)
\(R_{Leitung2}=\rho \cdot \frac l A= 17,86\cdot10^{-3}\ \frac{\Omega\cdot mm^2}{m}\cdot\frac{200\ m}{1,5\ mm^2}=2,38\ \Omega\)

Strom mit der 10m Leitung \(I_1\)
\(U = R_1\cdot I_1 \Leftrightarrow I_1=\frac{U}{R_1}=\frac{230\ V}{20,35\ \Omega+0,238\ \Omega}=\frac{230\ V}{20,588\ \Omega}=11,17\ A\)

Strom mit der 100m Leitung \(I_2\)
\(U = R_2\cdot I_2 \Leftrightarrow I_2=\frac{U}{R_2}=\frac{230\ V}{20,35\ \Omega+2,38\ \Omega}=\frac{230\ V}{22,73\ \Omega}=10,12\ A\)

Spannungsabfall über die 10m Leitung \(U_1\)
\(U_1=R_{Leitung1}\cdot I_1=238\ m\Omega\cdot 11,17\ A=0,238\ \Omega\cdot 11,17\ A=2.66\ V\approx 3\ V\)

Spannungsabfall über die 100m Leitung \(U2\)
\(U_2=R_{Leitung2}\cdot I_2=2,38\ \Omega\cdot 10,12\ A=24,09\ V\)

Leistung der Heizung mit 10m Leitung \(P_1\):
\(P_1=(U-U_1)\cdot I_1= (230\ V-3\ V)\cdot 11,17\ A=2535,6\ W\approx2536\ W\)

Leistung der Heizung mit 100m Leitung \(P_2\):
\(P_2=(U-U_2)\cdot I_2=(230\ V-24,09\ V)\cdot 10,10\ A=205,91\ V\cdot 10,12\ A=2083,8\ W\approx 2084\ W\)

Antwort:
Auf der ersten Baustelle erzielt die Heizung eine Leistung von 2536 W. Auf der zweiten Baustelle erzielt sie nur noch eine Leistung von 2084 W.

Aufgabe 3

Ermittle, welche elektrischen Größen für den Leistungsverlust verantwortlich waren.

Über die längere Leitung fällt eine höhere Spannung ab. Diese Spannung steht an der Heizung nicht mehr zur Verfügung.

Zusätzlich wird der Strom durch den zusätzlichen Leitungswiderstand vermindert.

Die Verminderung von Strom und Spannung führt an der Heizung zur Leistungsminderung.